Konsep Dan Pola Soal Bola Konduktor (Hukum Gauss) – Fisika Sma Kelas 12
Hukum Gauss sanggup digunakan untuk menyeleksi besar lengan berkuasa medan listrik akhir muatan yang terdistribusi secara simetris. Pada bahan fisika Sekolah Menengan Atas kelas 12, aplikasi Hukum Gauss digunakan untuk menjalankan analisis medan listrik dan mempunyai potensi listrik pada bola konduktor. Bola konduktor mempunyai karakteristik muatan listrik yang tersebar di seluruh permukaannya secara homogen. Kondisi-kondisi yang perlu dimengerti untuk menjalankan analisis bola konduktor yakni posisi titik uji, yakni di dalam bola, di permukaan bola, dan di luar bola.
Hukum Gauss menyatakan bahwa jumlah fluks listrik dalam sebuah permukaan tertutup seimbang dengan jumlah muatan listrik yang dilingkupi (dibungkus) oleh permukaan tersebut $\left( Q \right)$. Secara lazim kekerabatan persamaan Hukum Gauss dinyatakan dalam persamaan 1 berikut ini.
$\int{E\,dA}=\frac{Q}{{{\varepsilon }_{o}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
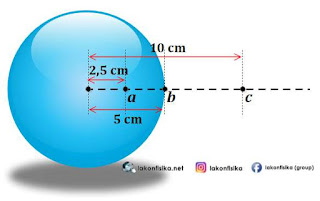
(b) titik berjarak $r=5\,cm$ dari sentra bola ($r=R$ atau di permukaan bola)
(c) titik berjarak $r=10\,cm$ dari sentra bola ($r>R$ atau di luar bola)
Hukum Gauss menyatakan bahwa jumlah fluks listrik dalam sebuah permukaan tertutup seimbang dengan jumlah muatan listrik yang dilingkupi (dibungkus) oleh permukaan tersebut $\left( Q \right)$. Secara lazim kekerabatan persamaan Hukum Gauss dinyatakan dalam persamaan 1 berikut ini.
$\int{E\,dA}=\frac{Q}{{{\varepsilon }_{o}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
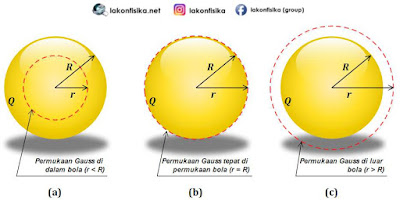
Untuk menyeleksi besar medan listrik yang disebabkan oleh bola konduktor (jari-jari yakni $R$), maka perlu diputuskan apalagi dahulu titik ujinya, yakni di dalam bola, di permukaan bola, atau di luar bola. Setelah itu gres kita buat permukaan Gauss pada masing-masing titik uji tersebut dengan jari-jari sebesar $r$. Gambar di atas menampilkan ilustrasi permukaan Gauss pada masing-masing tempat bola konduktor.
Sedangkan mempunyai potensi listrik diputuskan menurut keterkaitannya dengan medan listrik yaitu:
$\int\limits_{R}^{r}{dV}=\int\limits_{R}^{r}{E\,dr}\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right)$
1. Medan Listrik dan Potensial di dalam Bola Konduktor
Pada Gambar a, permukaan Gauss berada di dalam bola konduktor. Artinya tidak ada muatan yang dilingkupi (dibungkus) oleh permukaan Gauss $\left( Q=0 \right)$. Ingat bahwa muatan listrik bola konduktor tersebar cuma di permukaan bola, jadi tidak ada muatan di dalam bola konduktor. Jika nilai $Q=0$ dan biar persamaan 1 konsisten, maka nilai medan listrik mesti nol $\left( E=0 \right)$.
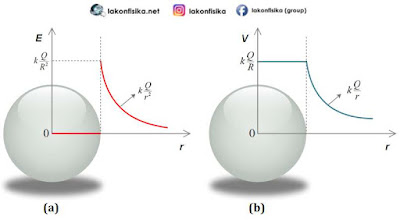
Makara sanggup ditarik kesimpulan bahwa besar lengan berkuasa medan listrik untuk titik di dalam bola konduktor $\left( r<R \right)$ niscaya bernilai nol $\left( E=0 \right)$.
Berdasarkan kekerabatan persamaan 2, untuk $E=0$ maka nilai ${{V}_{r}}={{V}_{R}}$. Makara nilai mempunyai potensi listrik di dalam bola konduktor adalah:
$V=k\frac{Q}{R}\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
2. Medan Listrik dan Potensial di permukaan Bola Konduktor
Pada Gambar b, permukaan Gauss berada sempurna di permukaan bola konduktor. Artinya muatan yang dilingkupi (dibungkus) oleh permukaan Gauss yakni sebesar $Q$. Ingat bahwa muatan listrik bola konduktor tersebar cuma di permukaan bola, jadi sempurna dilingkupi oleh bola konduktor. Berdasarkan keadaan fisis tersebut, maka persamaan 1 sanggup dianalisis selaku berikut.
$\int{E\,dA}=\frac{Q}{{{\varepsilon }_{o}}}$
$E\,A=\frac{Q}{{{\varepsilon }_{o}}}$
$E\,\left( 4\pi {{r}^{2}} \right)=\frac{Q}{{{\varepsilon }_{o}}}$ permukaan Gauss berupa bola, maka $A=4\pi {{r}^{2}}$.
$E\,=\frac{Q}{{{\varepsilon }_{o}}}\frac{1}{4\pi {{r}^{2}}}$
$E\,=\frac{1}{4\pi {{\varepsilon }_{o}}}\frac{Q}{{{r}^{2}}}$ dengan nilai $k=\frac{1}{4\pi {{\varepsilon }_{o}}}$ dan nilai $r=R$ (tepat di permukaan bola), maka:
$E=k\frac{Q}{{{R}^{2}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$
Potensial listrik di permukaan bola ditemukan menurut integrasi persamaan 2, sehingga ditemukan persamaan berikut ini.
$V=k\frac{Q}{R}\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right)$
3. Medan Listrik dan Potensial di luar Bola Konduktor
Pada Gambar c, permukaan Gauss lebih luas dari pada permukaan bola konduktor. Artinya seluruh bola konduktor terlingkupi oleh permukaan Gauss. Oleh lantaran itu muatan yang dilingkupi (dibungkus) oleh permukaan Gauss yakni sebesar $Q$. Berdasarkan keadaan fisis tersebut, maka persamaan 1 sanggup dianalisis dengan cara yang serupa menyerupai keadaan di permukaan bola. Bedanya cuma nilai $r\ne R$ tetapi $r>R$. Sehingga persamaan untuk menyeleksi medan listrik pada titik yang berjarak $r$ dari sentra bola adalah:
$E=k\frac{Q}{{{r}^{2}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 6 \right)$
Berdasarkan integrasi persamaan 2, mempunyai potensi listrik pada titik di luar bola konduktor menyerupai mempunyai potensi yang dihasilkan muatan titik. Makara bola dianggap selaku muatan titik, sehingga persamaan mempunyai potensi di luar bola konduktor adalah:
$V=k\frac{Q}{r}\quad \ldots \ldots \ldots \ldots \ldots \left( 7 \right)$
Agar lebih gampang dipahami, gambar di bawah ini menampilkan ilustrasi nilai medan listrik dan mempunyai potensi listrik untuk masing-masing area pada bola konduktor. Gambar a ialah grafik besar medan listrik kepada jarak titik dari sentra bola, sedangkan Gambar b ialah grafik mempunyai potensi listrik.
Contoh Soal Bola Konduktor
(1). Bola konduktor mempunyai jari-jari $5\,cm$ dengan muatan total sebesar $20\,\mu C$ yang tersebar merata. Tentukan medan dan mempunyai potensi listrik pada masing-masing titik berjarak: (a) $2,5\,cm$, (b) $5\,cm$, dan (c) $10\,cm$ dari sentra bola.
Jawab:
$E=0$
$V=k\frac{Q}{R}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{5\cdot {{10}^{-2}}}$
$V=3,6\cdot {{10}^{6}}\,volt$
(b) titik berjarak $r=5\,cm$ dari sentra bola ($r=R$ atau di permukaan bola)
$E=k\frac{Q}{{{R}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{{{\left( 5\cdot {{10}^{-2}} \right)}^{2}}}$
$E=7,2\cdot {{10}^{7}}\,{N}/{C}\;$
$V=k\frac{Q}{R}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{5\cdot {{10}^{-2}}}$
$V=3,6\cdot {{10}^{6}}\,volt$
(c) titik berjarak $r=10\,cm$ dari sentra bola ($r>R$ atau di luar bola)
$E=k\frac{Q}{{{r}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{{{\left( 10\cdot {{10}^{-2}} \right)}^{2}}}$
$E=1,8\cdot {{10}^{7}}\,{N}/{C}\;$
$V=k\frac{Q}{r}$
$V=9\cdot {{10}^{9}}\frac{20\cdot {{10}^{-6}}}{10\cdot {{10}^{-2}}}$
$V=1,8\cdot {{10}^{6}}\,volt$
(2). Bola tipis berongga mempunyai jari-jari 20 cm. Jika besar lengan berkuasa medan listrik pada sebuah titik di luar bola yang berjarak $10\,cm$ dari kulit bola yakni $8\times {{10}^{3}}\,{N}/{C}\;$, maka tentukan besar lengan berkuasa medan listrik pada: (a) titik yang berjarak $10\,cm$ dari sentra bola, (b) kulit bola, dan (c) titik di luar bola yang berjarak $15\,cm$ dari kulit bola.
Jawab:
Berdasarkan keadaan permulaan ${{r}_{p}}=30\,cm$ dari sentra bola (titik P di luar bola), maka sanggup diputuskan apalagi dahulu nilai muatan total:
$E=k\frac{Q}{r_{p}^{2}}$
$Q=E\frac{r_{p}^{2}}{k}$
$Q=8\cdot {{10}^{3}}\frac{{{\left( 3\cdot {{10}^{-1}} \right)}^{2}}}{9\cdot {{10}^{9}}}$
$Q=8\cdot {{10}^{-8}}\,C$
(a) titik a dengan ${{r}_{a}}=10\,cm$ dari sentra bola (${{r}_{a}}<R$ atau di dalam bola)
$E=0$
(b) titik a dengan ${{r}_{b}}=20\,cm$ dari sentra bola (${{r}_{b}}=R$ atau di permukaan bola)
$E=k\frac{Q}{{{R}^{2}}}$
$E=9\cdot {{10}^{9}}\frac{8\cdot {{10}^{-8}}}{{{\left( 2\cdot {{10}^{-1}} \right)}^{2}}}$
$E=1,8\cdot {{10}^{4}}\,{N}/{C}\;$
(c) titik a dengan ${{r}_{c}}=35\,cm$ dari sentra bola (${{r}_{c}}>R$ atau di luar bola)
$E=k\frac{Q}{{{r}_{c}}^{2}}$
$E=9\cdot {{10}^{9}}\frac{8\cdot {{10}^{-8}}}{{{\left( 3,5\cdot {{10}^{-1}} \right)}^{2}}}$
$E=5,9\cdot {{10}^{3}}\,{N}/{C}\;$