Konsep Dan Teladan Soal Medan Listrik – Berpotensi Listrik – Fisika Sma Kelas 12
Setelah mempelajari Hukum Coulomb, pasti saja kita sudah paham bahwa gaya Coulomb ialah jenis gaya non kontak. Artinya ada tempat di sekeliling muatan listrik yang terpengaruh gaya Coulomb. Daerah di sekeliling muatan yang terpengaruh muatan listrik disebut selaku medan listrik. Kalau kita balik budi berpikirnya, sanggup dinyatakan bahwa jikalau ada muatan berada dalam suatu medan listrik, maka muatan tersebut akan mendapat Gaya Coulomb.
Medan listrik berhubungan dengan karakteristik individu setiap jenis muatan, bukan hasil interaksi antar muatan menyerupai gaya Coulomb. Pada bahan fisika Sekolah Menengan Atas kelas 12, akan dipelajari karakteristik individu dari muatan listrik, yakni medan listrik dan mempunyai potensi listrik. Medan listrik ialah jenis besaran vektor, jadi selain mempunyai nilai, medan listrik juga mempunyai arah. Sedangkan mempunyai potensi listrik ialah besaran skalar, artinya cuma mempunyai nilai saja.
$F=E\cdot {{q}_{uji}}$
$E=\frac{F}{{{q}_{uji}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Perlu dimengerti bahwa muatan uji $\left( {{q}_{uji}} \right)$ berperan selaku obyek yang terpengaruh oleh medan listrik dari suatu muatan listrik $\left( q \right)$. Karena nilai $F=k\frac{q\ {{q}_{uji}}}{{{r}^{2}}}$, kita sanggup penyesuaian persamaan 1 menjadi persamaan 2 berikut ini untuk menyeleksi mempunyai pengaruh medan listrik.
$E=\frac{k\frac{q\ {{q}_{uji}}}{{{r}^{2}}}}{{{q}_{uji}}}$ dengan mengeliminasi nilai ${{q}_{uji}}$, kita dapatkan:
$E=k\frac{q}{{{r}^{2}}}\quad \ldots \ldots \,\ldots \ldots \left( 2 \right)$
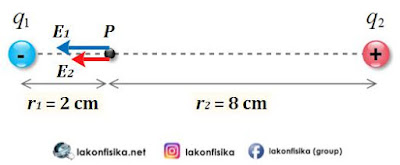
Gambar di atas ialah gambaran medan listrik yang terjadi di sekeliling muatan positif $\left( {{q}_{1}} \right)$ dan negatif $\left( {{q}_{2}} \right)$ . Arah medan listrik muatan positif senantiasa menjauhi muatan tersebut. Sedangkan muatan negatif mempunyai arah medan listrik menuju muatan tersebut. Jika tempatkan suatu muatan uji positif $\left( {{q}_{uji}} \right)$ di suatu titik, maka muatan uji akan terpengaruh medan listrik dari ${{q}_{1}}$ $\left( {{E}_{1}} \right)$ dan medan listrik dari ${{q}_{2}}$ $\left( {{E}_{2}} \right)$.
Pada ${{q}_{uji}}$, medan listrik ${{E}_{1}}$ mempunyai arah menjauhi ${{q}_{1}}$ dan medan listrik ${{E}_{2}}$ menuju ${{q}_{2}}$. Akibat efek medan-medan listrik tersebut, ${{q}_{uji}}$ mengalami gaya Coulomb masing-masing yakni ${{F}_{1}}$ dan ${{F}_{2}}$. Jika besar titik muatan uji tersebut berjarak ${{r}_{1}}$ dari ${{q}_{1}}$ dan berjarak ${{r}_{2}}$ dari ${{q}_{2}}$, maka masing-masing mempunyai pengaruh medan listrik adalah:
${{E}_{1}}=k\frac{{{q}_{1}}}{r_{1}^{2}}$ dan ${{E}_{2}}=k\frac{{{q}_{2}}}{r_{2}^{2}}$
Jika ingin diputuskan resultan medan listrik di tersebut, maka mesti digunakan prinsip resultan vektor menyerupai gambaran pada gambar di atas. Resultan mempunyai pengaruh medan listrik $\left( {{E}_{R}} \right)$ sanggup diputuskan dengan persamaan 3 berikut ini.
${{E}_{R}}=\sqrt{{{E}_{1}}^{2}+{{E}_{2}}^{2}+2\ {{E}_{1}}\ {{E}_{2}}\ \cos \alpha }\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
Hitung Nilai ${{E}_{1}}$
Hitung Nilai ${{E}_{2}}$
Hitung Nilai ${{E}_{A}}$
Medan listrik berhubungan dengan karakteristik individu setiap jenis muatan, bukan hasil interaksi antar muatan menyerupai gaya Coulomb. Pada bahan fisika Sekolah Menengan Atas kelas 12, akan dipelajari karakteristik individu dari muatan listrik, yakni medan listrik dan mempunyai potensi listrik. Medan listrik ialah jenis besaran vektor, jadi selain mempunyai nilai, medan listrik juga mempunyai arah. Sedangkan mempunyai potensi listrik ialah besaran skalar, artinya cuma mempunyai nilai saja.
1. Konsep Medan Listrik
Setiap jenis muatan listrik mempunyai medan listrik di sekitarnya. Untuk mengenali mempunyai pengaruh medan di suatu titik, kita sanggup menempatkan muatan uji $\left( {{q}_{uji}} \right)$ pada titik tersebut dan mengukur besar gaya Coulombnya. Muatan $\left( q \right)$ akan berinteraksi dengan muatan uji $\left( {{q}_{uji}} \right)$ sesuai desain Hukum Coulomb. Kuat medan listrik ialah gaya Coulomb per muatan uji tersebut. Secara matematis, mempunyai pengaruh medan listrik sanggup diputuskan dengan persamaan 1 berikut ini.$F=E\cdot {{q}_{uji}}$
$E=\frac{F}{{{q}_{uji}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$
Perlu dimengerti bahwa muatan uji $\left( {{q}_{uji}} \right)$ berperan selaku obyek yang terpengaruh oleh medan listrik dari suatu muatan listrik $\left( q \right)$. Karena nilai $F=k\frac{q\ {{q}_{uji}}}{{{r}^{2}}}$, kita sanggup penyesuaian persamaan 1 menjadi persamaan 2 berikut ini untuk menyeleksi mempunyai pengaruh medan listrik.
$E=\frac{k\frac{q\ {{q}_{uji}}}{{{r}^{2}}}}{{{q}_{uji}}}$ dengan mengeliminasi nilai ${{q}_{uji}}$, kita dapatkan:
$E=k\frac{q}{{{r}^{2}}}\quad \ldots \ldots \,\ldots \ldots \left( 2 \right)$
 |
| Ilustrasi Medan Listrik pada Muatan Positif dan Negatif |
Gambar di atas ialah gambaran medan listrik yang terjadi di sekeliling muatan positif $\left( {{q}_{1}} \right)$ dan negatif $\left( {{q}_{2}} \right)$ . Arah medan listrik muatan positif senantiasa menjauhi muatan tersebut. Sedangkan muatan negatif mempunyai arah medan listrik menuju muatan tersebut. Jika tempatkan suatu muatan uji positif $\left( {{q}_{uji}} \right)$ di suatu titik, maka muatan uji akan terpengaruh medan listrik dari ${{q}_{1}}$ $\left( {{E}_{1}} \right)$ dan medan listrik dari ${{q}_{2}}$ $\left( {{E}_{2}} \right)$.
Pada ${{q}_{uji}}$, medan listrik ${{E}_{1}}$ mempunyai arah menjauhi ${{q}_{1}}$ dan medan listrik ${{E}_{2}}$ menuju ${{q}_{2}}$. Akibat efek medan-medan listrik tersebut, ${{q}_{uji}}$ mengalami gaya Coulomb masing-masing yakni ${{F}_{1}}$ dan ${{F}_{2}}$. Jika besar titik muatan uji tersebut berjarak ${{r}_{1}}$ dari ${{q}_{1}}$ dan berjarak ${{r}_{2}}$ dari ${{q}_{2}}$, maka masing-masing mempunyai pengaruh medan listrik adalah:
${{E}_{1}}=k\frac{{{q}_{1}}}{r_{1}^{2}}$ dan ${{E}_{2}}=k\frac{{{q}_{2}}}{r_{2}^{2}}$
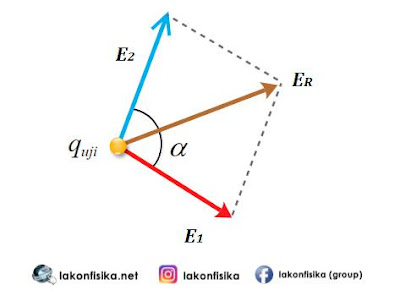 |
| Ilustrasi Resultan Medan Listrik |
Jika ingin diputuskan resultan medan listrik di tersebut, maka mesti digunakan prinsip resultan vektor menyerupai gambaran pada gambar di atas. Resultan mempunyai pengaruh medan listrik $\left( {{E}_{R}} \right)$ sanggup diputuskan dengan persamaan 3 berikut ini.
${{E}_{R}}=\sqrt{{{E}_{1}}^{2}+{{E}_{2}}^{2}+2\ {{E}_{1}}\ {{E}_{2}}\ \cos \alpha }\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$
Contoh Soal Medan Listrik
(1). Tentukan besar dan arah mempunyai pengaruh medan listrik pada titik P yang berjarak 30 cm dari muatan $Q\left( -3\times {{10}^{-6}}C \right)$.
Jawab:
${{E}_{p}}=k\frac{Q}{{{r}^{2}}}$
${{E}_{p}}=9\cdot {{10}^{9}}\frac{3\cdot {{10}^{-6}}}{{{\left( 3\cdot {{10}^{-1}} \right)}^{2}}}$
${{E}_{p}}=9\cdot {{10}^{5}}\ {}^{N}/{}_{C}$
Kaprikornus besar mempunyai pengaruh medan listrik di titik P yakni $9\cdot {{10}^{5}}\ {}^{N}/{}_{C}$ dengan arah menuju muatan $Q$.
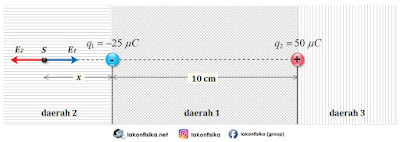
(2). Dua muatan listrik terpisah sejauh 10 cm. Masing-masing mempunyai muatan sebesar ${{q}_{1}}=-25\ \mu C$ dan ${{q}_{2}}=+50\ \mu C$. Jika di antara kedua muatan tersebut (titik P) ditaruh suatu elektron, dengan jarak 2 cm dari muatan ${{q}_{1}}$, maka tentukan:
a. kuat medan listrik di titik P
b. percepatan permulaan elektron sesaat sehabis diposisikan di titik P$\left( {{m}_{e}}=9\times {{10}^{-31}}\ kg\ ;\ \quad {{q}_{e}}=-1,6\times {{10}^{-19}}C \right)$
c. posisi titik dengan mempunyai pengaruh medan listrik total nol
Jawab:
a. Kita pastikan arah medan listrik oleh masing-masing muatan ${{q}_{1}}$ dan ${{q}_{2}}$, dengan ${{E}_{1}}$ dan ${{E}_{2}}$ searah menuju muatan ${{q}_{1}}$.
${{E}_{p}}={{E}_{1}}+{{E}_{2}}$
${{E}_{p}}=k\frac{{{q}_{1}}}{r_{1}^{2}}+k\frac{{{q}_{2}}}{r_{2}^{2}}$
${{E}_{p}}=k\left( \frac{{{q}_{1}}}{r_{1}^{2}}+\frac{{{q}_{2}}}{r_{2}^{2}} \right)$
${{E}_{p}}=9\cdot {{10}^{9}}\left( \frac{25\cdot {{10}^{-6}}}{{{\left( 2\cdot {{10}^{-2}} \right)}^{2}}}+\frac{50\cdot {{10}^{-6}}}{{{\left( 8\cdot {{10}^{-2}} \right)}^{2}}} \right)$
${{E}_{p}}=6,3\cdot {{10}^{8}}\ {}^{N}/{}_{C}$
b. Untuk menyeleksi percepatan elektron, kita kombinasikan gaya Coulomb dan Hukum Newton II.
$F={{m}_{e}}\ a$
${{E}_{p}}\cdot {{q}_{e}}={{m}_{e}}\cdot a$
$a=\frac{{{E}_{p}}\cdot {{q}_{e}}}{{{m}_{e}}}$
$a=\frac{\left( 6,3\cdot {{10}^{8}} \right)\cdot \left( 1,6\cdot {{10}^{-19}} \right)}{9\cdot {{10}^{-31}}}$
$a=\frac{\left( 6,3\cdot {{10}^{8}} \right)\cdot \left( 1,6\cdot {{10}^{-19}} \right)}{9\cdot {{10}^{-31}}}=1,1\cdot {{10}^{20}}\ {}^{m}/{}_{{{s}^{2}}}$
c. Kita mesti ketahui bahwa mempunyai pengaruh medan listrik bernilai nol jikalau dua medan listrik saling bertentangan arah dan sama besar. Untuk menyeleksi posisi titik dengan medan listrik nol, kita mesti perkirakan masing-masing arah medan listrik akhir masing-masing muatan. Masing-masing medan listrik tersebut mesti saling bertentangan arah, ingat syarat resultan agar nilainya nol.
Kita sanggup kategorikan menjadi 3 tempat menyerupai gambar di atas. Pada tempat 1, di sepanjang garis penghubung ${{q}_{1}}$ dan ${{q}_{2}}$ (garis putus-putus), maka dua medan listrik akan searah menuju ${{q}_{1}}$, jadi tidak mungkin resultan akan nol. Jika titik $S$ ditaruh pada tempat 2 dan 3, maka masing-masing medan listrik akan bertentangan arah. Nah, selanjutnya, kita tinggal pilih tempat 2 dengan argumentasi besar medan listrik berbanding lurus dengan muatan, dan berbanding terbalik dengan kuadrat jarak. Karena ${{q}_{1}}<{{q}_{2}}$ dan ${{r}_{2}}>{{r}_{1}}$ , akan sungguh mungkin nilai ${{E}_{2}}={{E}_{1}}$.
${{E}_{2}}={{E}_{1}}$
$k\frac{{{q}_{2}}}{{{\left( {{r}_{2}} \right)}^{2}}}=k\frac{{{q}_{1}}}{{{\left( {{r}_{1}} \right)}^{2}}}$
$\frac{{{q}_{2}}}{{{\left( {{r}_{2}} \right)}^{2}}}=\frac{{{q}_{1}}}{{{\left( {{r}_{1}} \right)}^{2}}}$
$\frac{50}{{{\left( 10-x \right)}^{2}}}=\frac{25}{{{\left( x \right)}^{2}}}$ (nilai satuan tidak perlu dikonversi ke SI alasannya yakni kita tinggal pakai prinsip perbandingan matematika)
$\sqrt{\frac{50}{{{\left( 10-x \right)}^{2}}}}=\sqrt{\frac{25}{{{\left( x \right)}^{2}}}}$ (dengan teknik matematis kita akar kedua ruas agar lebih sederhana)
$\frac{5\sqrt{2}}{10-x}=\frac{5}{x}$
$10-x=\sqrt{2}\ x$
$x+\sqrt{2}\,x=10$
$x=\frac{10}{\left( 1+\sqrt{2} \right)}\ cm$
Kaprikornus posisi titik $S$ yakni $\frac{10}{\left( 1+\sqrt{2} \right)}\ cm$ di sebelah kiri ${{q}_{1}}$.
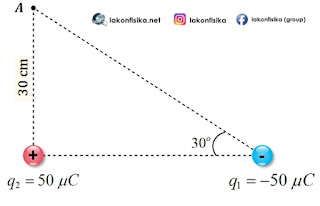
(3). Tentukan mempunyai pengaruh medan listrik total pada titik A akhir efek muatan ${{q}_{1}}$ dan ${{q}_{2}}$!
Jawab:
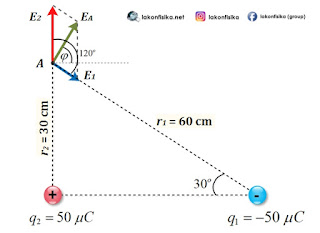
Langkah pertama yakni kita pastikan medan listrik akhir masing-masing muatan di titik A.
Hitung Nilai ${{E}_{1}}$
${{E}_{1}}=k\frac{{{q}_{1}}}{r_{1}^{2}}$
${{E}_{1}}=9\cdot {{10}^{9}}\frac{50\cdot {{10}^{-6}}}{{{\left( {{6.10}^{-1}} \right)}^{2}}}$
${{E}_{1}}=1,25\cdot {{10}^{6}}\ {}^{N}/{}_{C}$
Hitung Nilai ${{E}_{2}}$
${{E}_{2}}=k\frac{{{q}_{2}}}{r_{2}^{2}}$
${{E}_{2}}=9\cdot {{10}^{9}}\frac{50\cdot {{10}^{-6}}}{{{\left( {{3.10}^{-1}} \right)}^{2}}}$
${{E}_{2}}=5\cdot {{10}^{6}}\ {}^{N}/{}_{C}$
Hitung Nilai ${{E}_{A}}$
${{E}_{A}}=\sqrt{E_{1}^{2}+E_{2}^{2}+2\,{{E}_{1}}\,{{E}_{2}}\,\cos {{120}^{o}}}$
${{E}_{A}}=\sqrt{{{\left( 1,25\cdot {{10}^{6}} \right)}^{2}}+{{\left( 5\cdot {{10}^{6}} \right)}^{2}}+2\,\left( 1,25\cdot {{10}^{6}} \right)\,\left( 5\cdot {{10}^{6}} \right)\,\left( -\frac{1}{2} \right)}$
${{E}_{A}}={{10}^{6}}\sqrt{{{\left( 1,25 \right)}^{2}}+{{\left( 5 \right)}^{2}}-\,\left( 1,25 \right)\,\left( 5 \right)\,}$
${{E}_{A}}={{10}^{6}}\sqrt{{{\left( 1,25 \right)}^{2}}+{{\left( 5 \right)}^{2}}-\,\left( 1,25 \right)\,\left( 5 \right)\,}$
${{E}_{A}}=4,5\cdot {{10}^{6}}\,{}^{N}/{}_{C}$
2. Konsep Fluks Listrik dan Hukum Gauss
Hukum Gauss meliputi desain Fluks Listrik, yakni ialah garis medan listrik yang menembus suatu luasan secara tegak lurus. Medan listrik homogen $\left( E \right)$ yang menembus suatu luasan $\left( A \right)$, diilustrasikan pada gambar di bawah.
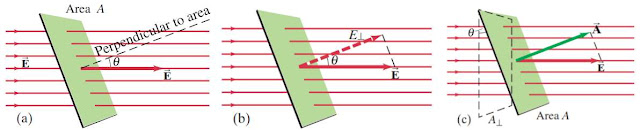 |
| Ilustrasi Konsep Hukum Gauss |
Sudut $\theta $ ialah sudut terbuat antara arah medan listrik $\left( E \right)$ dan garis yang tegak lurus bidang luasan $\left( A \right)$ atau garis wajar bidang. Untuk mendapat fluks listrik, medan listrik diuraikan menjadi unsur medan listrik yang tegak lurus bidang (sejajar garis wajar bidang) yakni ${{E}_{\bot }}=E\cos \theta $. Atau sanggup juga dicari unsur bidang luasan $\left( A \right)$ yang tegak lurus $E$, yakni ${{A}_{\bot }}=A\cos \theta $. Berdasarkan kondisi-kondisi tersebut, besar fluks listrik $\left( {{\Phi }_{E}} \right)$ sanggup diputuskan dengan persamaan 4.
${{\Phi }_{E}}=\left( {{E}_{\bot }}\ A \right)=\left( E\ {{A}_{\bot }} \right)=E\ A\ \cos \theta \quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$
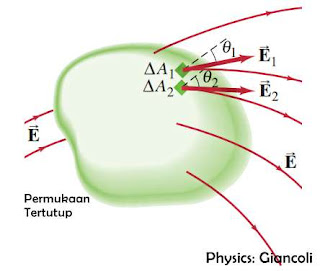 |
| Ilustrasi Hukum Gauss pada Permukan Tertutup |
Secara lebih khusus, Hukum Gauss meliputi seluruh fluks listrik yang menembus luasan permukaan tertutup (closed surface). Permukaan tertutup tersebut mempunyai bentuk tidak beraturan dan membungkus ruang kosong di dalamnya. Kita sanggup menghasilkan potongan-potongan kecil yang berupa bidang datar seluas $\Delta A$, menyerupai gambaran gambar di atas. Jika masing-masing luasan kecil, umpamanya $\Delta {{A}_{1}}$ dan $\Delta {{A}_{2}}$ ditembus oleh masing-masing medan listrik ${{E}_{1}}$ dan ${{E}_{2}}$, maka fluks total dalam permukaan tertutup tersebut adalah:
${{\Phi }_{E}}={{E}_{1}}A\cos {{\theta }_{1}}+{{E}_{2}}A\cos {{\theta }_{2}}+... $
${{\Phi }_{E}}=\sum{E\,\Delta A\cos \theta }$
${{\Phi }_{E}}=\sum{{{E}_{\bot }}\,\Delta A}$
Hukum Gauss menyatakan bahwa jumlah fluks listrik dalam suatu permukaan tertutup sepadan dengan jumlah muatan listrik yang dilingkupi (dibungkus) oleh permukaan tersebut $\left( Q \right)$. Hukum Gauss sanggup dinyatakan dengan persamaan 5 berikut ini.
$\sum {{E}_{\bot }}\Delta A=\frac{Q}{{{\varepsilon }_{o}}}\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right)$